Some things are hard to teach. Like good geometric visualization, or essentially, geometric intuition. How do you sketch a solid described in terms of algebraic curves and surfaces? How do you visualize the intersection of several surfaces in three dimensions? More importantly, how do you teach someone to do this?
In one class, I have to teach students to find volumes of solids of revolution. Years ago I found out these students have trouble making a sketch of a solid of revolution. Not because they lack prerequisite math skills (well, OK, sometimes because of that too), but because they lack the prerequisite drawing skills, and the essential geometric intuition that goes with them.
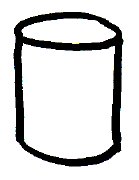
How do you draw a cylinder? Well, here's one way:
I know the top is a circle, so I'll draw that. I know the sides are straight, so I draw that. And the bottom is flat, so I draw that. And here's the cylinder:

We can call that "art primitive", also sometimes known as Picasso. So maybe my students are primed to make way more money than I do, since this is how many of them draw three dimensional objects. (Actually I long ago resigned myself to the fact that my students will make way more than I do right out of college.) But if you're willing to accept the developments of the Renaissance, you can draw in perspective:
I know that the top and bottom are disks, BUT, because I'm looking across the disks, they will show up foreshortened, looking more like ellipses:
And now you have a drawing in perspective. (Note that I make no claims as to being an artistic master. In fact, in college I took a drawing class in which I think the professor would have been more interested in the first drawing than the second. Overall, I prefer the second, which belongs to a school of art a friend dubbed "Drawing Things That Look Like Things." While it may be frowned upon by professional artists, "Drawing Things That Look Like Things" is much more useful if you are trying to solve a problem involving geometric figures. Perspective is a good thing.)
I remember in grade school, we used to occassionally watch a guy on TV who gave half-hour drawing lessons. I don't remember his name, but he taught how to draw things "in perspective" by foreshortening, and also how to apply shading to make an object look more three dimensional, and other things like that. He was pretty thorough in each example about explaining (and showing) us just exactly what to do, and so my drawings usually turned out pretty decent by the end of the show.
I think part of the difficulty my students have is that they never got this kind of instruction in grade school, so ideas about how to sketch a three-dimensional object are kind of foreign. (Perhaps another unfortunate side effect of eliminating subjects like art from the curriculum so as to spend more time learning to take bubble-in tests?) But that makes it harder for them to see three dimensional objects, too. I realized years ago that part of what they needed were basic drawing lessons, and so I often give some quick and dirty practical tips for drawing the figures. As a result, the pictures come out a little better, and I hope this helps them visualize the regions they're working with.
I give them some other tips, and of course practice helps too, so I tend to encourage them to try lots of examples and draw lots of pictures. But ultimately, I'm not teaching a technique or an algorithm, I'm trying to teach them how to see how three dimensional objects interact in space. And that's really tough.
No comments:
Post a Comment